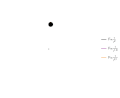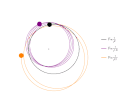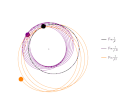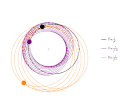ep = {0, 0};
me = 5;
mp = {{0, 5}, {0, 5}, {0, 5}};
acc = {me (ep - mp[[1]])/(Norm[ep - mp[[1]]]^1 Norm[ep - mp[[1]]]^2), me (ep - mp[[2]])/(Norm[ep - mp[[2]]]^1 Norm[ep - mp[[2]]]^1.9), me (ep - mp[[3]])/(Norm[ep - mp[[3]]]^1 Norm[ep - mp[[3]]]^2.1)};
mv = mv = {{Sqrt[Abs[Norm[acc[[1]] ] Norm[mp[[1]] - ep] ]], 0.2}, {Sqrt[Abs[Norm[acc[[1]] ] Norm[mp[[1]] - ep] ]], 0.2}, {Sqrt[Abs[Norm[acc[[1]] ] Norm[mp[[1]] - ep] ]], 0.2}};
dt = 0.2;
mpold = mp;
mp = mpold + mv dt + acc/2 dt^2;
evo = Reap[Do[
      acc = {me (ep - mp[[1]])/(Norm[ep - mp[[1]]]^1 Norm[ep - mp[[1]]]^2), 
        me (ep - mp[[2]])/(Norm[ep - mp[[2]]]^1 Norm[ep - mp[[2]]]^1.9), 
        me (ep - mp[[3]])/(Norm[ep - mp[[3]]]^1 Norm[ep - mp[[3]]]^2.1)};
      mpoldold = mpold;
      mpold = mp;
      mp = 2 mpold - mpoldold + acc dt^2;
      Sow[mp];
      , {1500}];][[2, 1]];
plots = Table[
   Legended[
    Graphics[{Gray, Disk[ep, 0.1 ],
      Purple, Disk[evo[[j, 2]], 0.5 ], Line[evo[[1 ;; j, 2]] ]
      ,
      Orange, Disk[evo[[j, 3]], 0.5 ], Line[evo[[1 ;; j, 3]] ]
      ,
      Black, Disk[evo[[j, 1]], 0.5 ], Line[evo[[1 ;; j, 1]] ]
      },
     PlotRange -> {{-10, 10}, {-10, 10}}, Frame -> False], LineLegend[{Black, Purple, Orange}, {"F\[Proportional]\!\(\*FractionBox[\(1\), \SuperscriptBox[\(r\), \(2\)]]\)", "F\[Proportional]\!\(\*FractionBox[\(1\), SuperscriptBox[\(r\), \(1.9\)]]\)", "F\[Proportional]\!\(\*FractionBox[\(1\), SuperscriptBox[\(r\), \(2.1\)]]\)"}] ]
   , {j, 1, Dimensions[evo][[1]]}];
ListAnimate[plots[[1 ;; -1 ;; 5]] ]